소개
수학계에서 가장 오랫동안 풀리지 않은 문제 중 하나인 리만 가설(Riemann Hypothesis)에 대해 이야기해보려고 합니다. 리만 가설은 1859년 독일 수학자 베른하르트 리만이 제안한 가설로, 현재까지도 해결되지 않은 문제 중 하나입니다.
리만 가설이란?
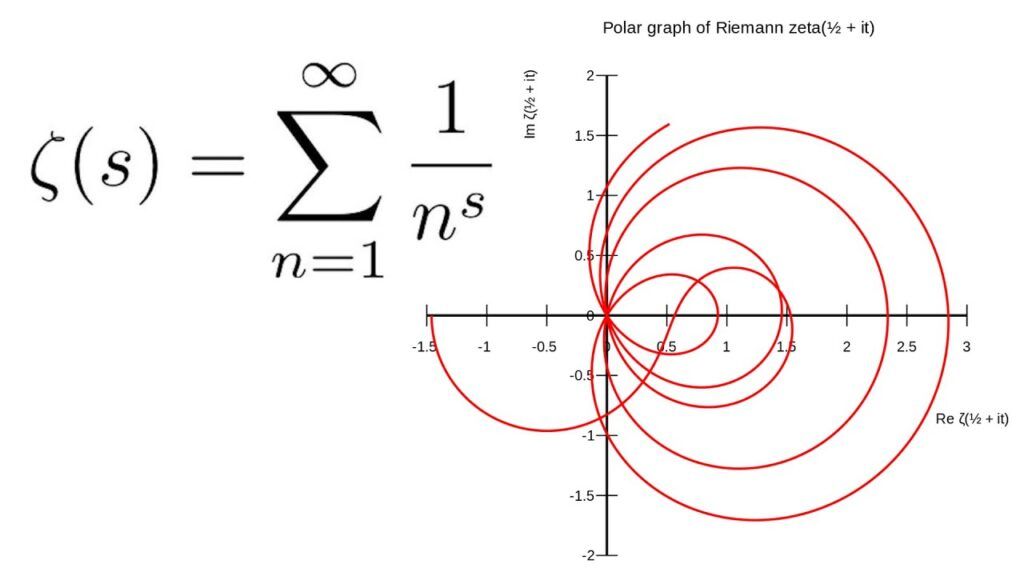
리만 가설은 직관적으로 말하자면, 모든 자연수의 집합에서 0과 1 사이에 있는 소수들의 분포를 나타내는 함수인 제타 함수의 모든 비자연수 해가 1/2 + it 형태의 복소수 t를 가진다는 가설입니다. 다소 추상적이고 어렵게 느껴질 수 있지만, 매우 간단히 말하자면, 소수들의 분포와 관련된 문제입니다.
리만 가설의 중요성
리만 가설은 암호학 분야에서 매우 �중요한 개념입니다. 현재 RSA 알고리즘은 소인수분해가 어렵다는 점에 기반하여 보안성이 보장됩니다. 그러나 RSA 알고리즘은 여러 가지 다른 알고리즘과 함께 사용되어 보안성을 더욱 강화합니다. 이때, RSA 알고리즘의 보안성은 소수들의 분포와 관련된 문제인 리만 가설에 의해 보장됩니다. 이 가설은 1859년에 프랑스 수학자 리만에 의해 제시되었으며, 소수들의 분포와 관련된 이론을 기반으로 하고 있습니다. 리만 가설은 아직 증명되지 않았지만, 수학계에서는 여전히 많은 연구가 진행되고 있습니다. 이 가설이 해결되면, 암호학 분야에서 새로운 알고리즘을 개발하는 데 적용될 수 있으며, 이를 통해 암호학 분야에서 더 나은 보안성을 제공할 수 있습니다. 따라서, 리만 가설은 암호학 분야에서 매우 중요한 의미를 지닐 것입니다.
리만 가설의 해결 가능성
리만 가설의 해결 가능성은 아직까지도 높지 않습니다. 하지만, 리만 가설은 지금까지 다양한 수학자들에 의해 많은 노력과 연구가 이루어져 왔습니다. 이제까지 알려진 모든 증거들은 리만 가설을 지지합니다. 그렇기 때문에, 리만 가설이 참이라는 것은 매우 높은 확률로 예상됩니다.
리만 가설 증명에 도전한 수학자들
리만 가설은 1859년에 독일 수학자 리만에 의해 제기된 가설입니다. 이 가설은 자연수의 수열을 이용하여 소수의 분포를 나타내는 것으로, 소수가 어떻게 분포하는지에 대한 연구와 관련이 있습니다. 이 가설은 지금까지 증명되지 않았고, 많은 수학자들이 이를 증명하기 위해 노력해왔습니다. 그 중에서도 가장 유명한 사람은 2002년에 필즈상을 수상한 러시아의 수학자 페렐만입니다. 그 외에도 앤드루 와일즈, 리차드 테일러, 엘리오트 해롤드 등 많은 수학자들이 리만 가설 증명에 도전했으며, 아직까지도 연구가 계속되고 있습니다. 최근에는 머신러닝 등의 기술을 이용하여 이 가설을 증명하려는 연구도 진행되고 있습니다.
리만 가설과 관련 있는 흥미로운 이야기
리만 가설은 아직까지 풀리지 않은 문제 중 하나입니다. 이에 대한 다양한 이야기가 있습니다. 2000년 클레이 수학 연구소에서는, 리만 가설을 해결한 사람에게 백만 달러의 상금을 준다는 소식이 전해졌습니다. 하지만, 아직까지도 리만 가설은 해결되지 않았기 때문에, 이 상금은 여전히 소유자를 찾지 못하고 있습니다. 이 가설이 풀리게 된다면, 수학계에 큰 발전을 가져올 것입니다. 이 가설에 대한 다양한 연구들이 진행되고 있으며, 이를 통해 수학계의 지식이 점차 더욱 발전하고 있습니다. 또한, 이 가설의 해결을 위해 수많은 수학자들이 노력하고 있으며, 그들의 노력과 열정은 이 가설의 해결에 큰 도움이 될 것입니다.
마무리
리만 가설은 1859년에 발표된 이래로, 수학계에서 가장 도전적인 문제 중 하나로 자리 잡았습니다. 이 문제는 현재까지도 풀리지 않은 문제 중 하나이며, 수많은 수학자들이 이 문제를 해결하기 위해 노력하고 있습니다. 많은 수학자들이 이 문제를 해결하기 위해 열심히 노력하고 있지만, 이 문제는 여전히 풀리지 않았습니다. 따라서, 새로운 접근법이 필요합니다. 이러한 노력들은 다양한 방식으로 이루어지고 있으며, 컴퓨터 프로그램을 사용한 방식이나 새로운 수학적 기법을 개발하는 방식 등이 있습니다. 이러한 노력들은 리만 가설을 해결하는 데 아주 중요합니다.
리만 가설이 해결되면, 수학계뿐만 아니라 물리학, 공학, 경제학 등 다양한 분야에서 중��요한 영향을 끼치게 될 것입니다. 예를 들어, 암호학 분야에서 안전한 암호를 만드는 데에 적용될 수 있을 것입니다. 또한, 이 문제를 해결하면 우주 탐사 분야에서도 중요한 역할을 할 수 있습니다. 이러한 이유로, 리만 가설은 여전히 수학계에서 가장 중요한 문제 중 하나로 여겨지며, 수많은 수학자들이 이 문제를 해결하기 위해 노력하고 있습니다. 이러한 노력들은 우리의 지식과 이해를 더욱 넓혀줄 것입니다.